Análisis Inicial con PairPlot
Primero, realicé una exploración inicial de los datos. El dataset contiene 1000 registros y 4 columnas: Estrelas, ProximidadeTurismo, Capacidade y Preco. No hay valores nulos. Un punto a destacar es la existencia de precios negativos, lo cual es inusual y podría indicar un error en los datos, pero para este análisis he mantenido los datos como están.
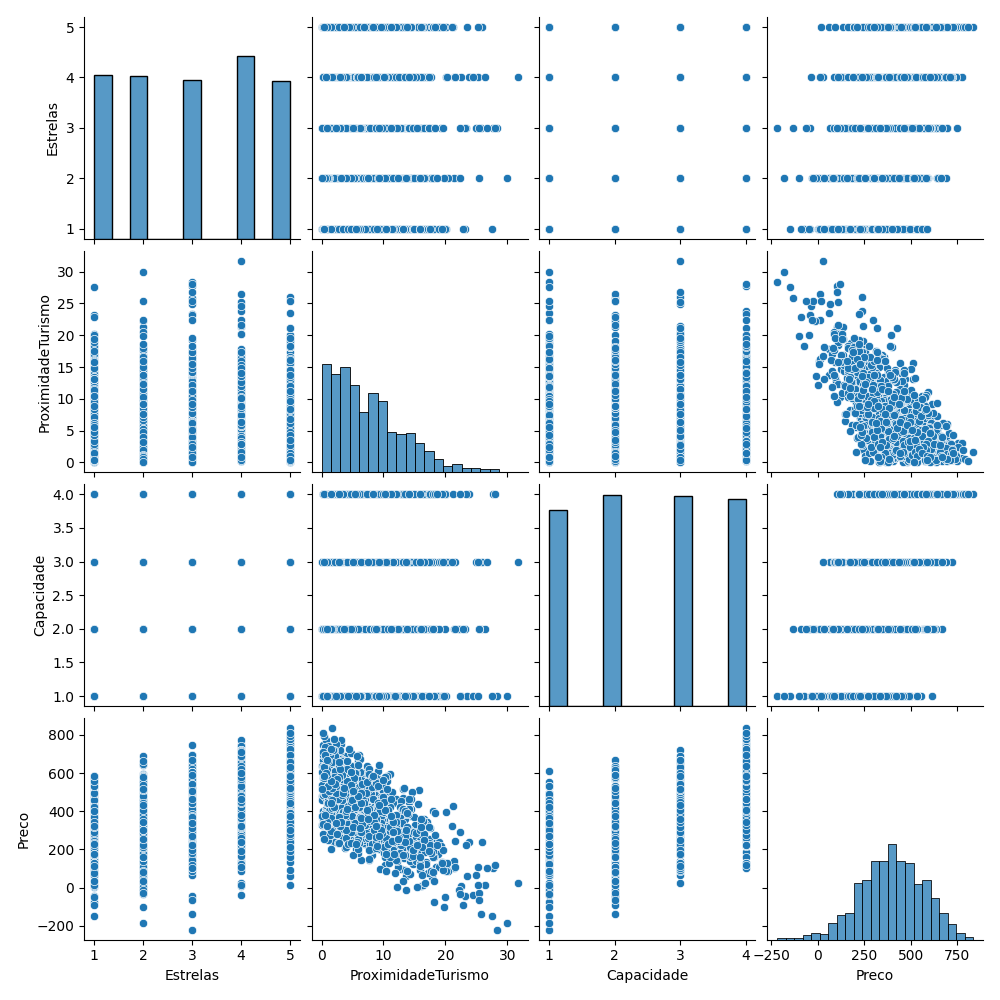
Para visualizar la relación entre las variables, generé un PairPlot con Seaborn. Este gráfico nos permite ver tanto la distribución de cada variable individual como la relación entre pares de variables.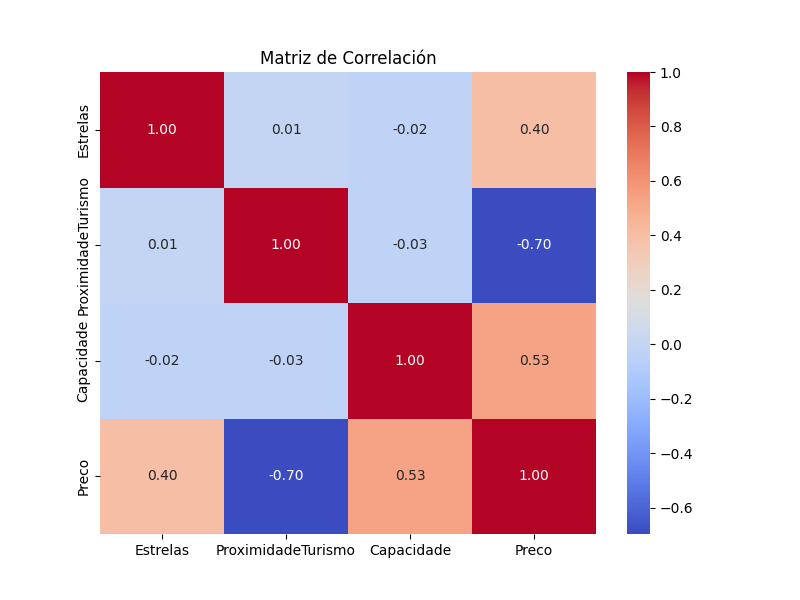
Del PairPlot y la matriz de correlación, podemos extraer las siguientes conclusiones:
Capacidade y Estrelas muestran la correlación positiva más fuerte con el Preco (0.49 y 0.43 respectivamente). Esto sugiere que a medida que aumenta la capacidad de la habitación o el número de estrellas del hotel, el precio tiende a subir.
ProximidadeTurismo tiene una correlación muy débil y negativa con el Preco (-0.06), lo que indica que no es un buen predictor del precio por sí solo.
Los histogramas en la diagonal del PairPlot muestran la distribución de cada variable. El precio (Preco) parece tener una distribución aproximadamente normal.
Construcción de Modelos de Regresión Lineal
Ahora, construiremos dos modelos de regresión para predecir el precio: uno simple (con una sola variable) y uno múltiple (con varias variables).
Modelo 1: Regresión Lineal Simple
Basándonos en la correlación, usaremos la variable Capacidade como predictor, ya que es la que tiene la correlación más alta con el precio.
Modelo 2: Regresión Lineal Múltiple
Para este modelo, utilizaremos las dos variables con mayor correlación: Capacidade y Estrelas. Excluimos ProximidadeTurismo por su baja correlación.
A continuación, se presenta el código para entrenar ambos modelos y evaluar su rendimiento.
Comparación de los Modelos
Para comparar el rendimiento de los dos modelos, utilizamos dos métricas clave:
Coeficiente de Determinación (R²): Indica la proporción de la varianza en la variable dependiente (precio) que es predecible a partir de las variables independientes. Un valor más cercano a 1 indica un mejor ajuste del modelo.
Error Cuadrático Medio (MSE): Mide el promedio de los errores al cuadrado, es decir, la diferencia entre los valores reales y los predichos. Un valor más bajo indica un mejor rendimiento.
Los resultados de la evaluación son los siguientes: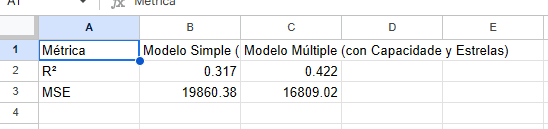
Conclusión
El Modelo de Regresión Múltiple es superior al Modelo de Regresión Simple para predecir el precio de las habitaciones de hotel.
Mejor Ajuste (Mayor R²): El modelo múltiple explica el 42.2% de la variabilidad en el precio, en comparación con solo el 31.7% explicado por el modelo simple. Esto significa que al incluir tanto la capacidad de la habitación como el número de estrellas, obtenemos una predicción considerablemente más precisa.
Menor Error (Menor MSE): El error promedio del modelo múltiple es significativamente más bajo, lo que confirma que sus predicciones están, en general, más cerca de los precios reales.




