Primera Etapa: Verificación de Multicolinealidad (VIF)
Para detectar la multicolinealidad entre las variables predictoras (AT, V, AP, RH), construí un modelo de regresión lineal y calculé el Factor de Inflación de la Varianza (VIF) para cada una.
El VIF mide qué tanto se infla la varianza de un coeficiente de regresión estimado si sus variables predictoras están correlacionadas. Una regla general común es que un VIF > 5 indica un nivel de multicolinealidad que podría ser problemático.
Resultados del VIF
Variable VIF
AT (Temperatura Ambiente) 5.98
V (Vacío de Escape) 3.94
RH (Humedad Relativa) 1.71
AP (Presión Atmosférica) 1.45
Export to Sheets
Análisis y Medidas a Tomar
La variable AT (Temperatura Ambiente) tiene un valor VIF de 5.98, lo que sugiere la presencia de una multicolinealidad moderada. Esto indica que AT está correlacionada con una o más de las otras variables predictoras.
El resto de las variables (V, RH, AP) tienen valores de VIF bajos, lo que indica que no presentan problemas de multicolinealidad.
¿Qué medidas se pueden tomar?
Investigar la Correlación: Podríamos crear una matriz de correlación para ver con qué otra variable está más fuertemente correlacionada AT.
Eliminar la Variable: Una opción común sería eliminar la variable AT del modelo y volver a entrenarlo para ver si el rendimiento se mantiene y los VIFs se estabilizan.
Combinar Variables: En algunos casos, se podrían combinar las variables correlacionadas en una sola.
Aceptar el Modelo: Dado que la multicolinealidad es moderada y el R-cuadrado del modelo es muy alto (0.929), se podría decidir mantener el modelo como está, asumiendo que el objetivo principal es la predicción y no la interpretación de los coeficientes individuales.
Segunda Etapa: Análisis de Residuos (Heterocedasticidad)
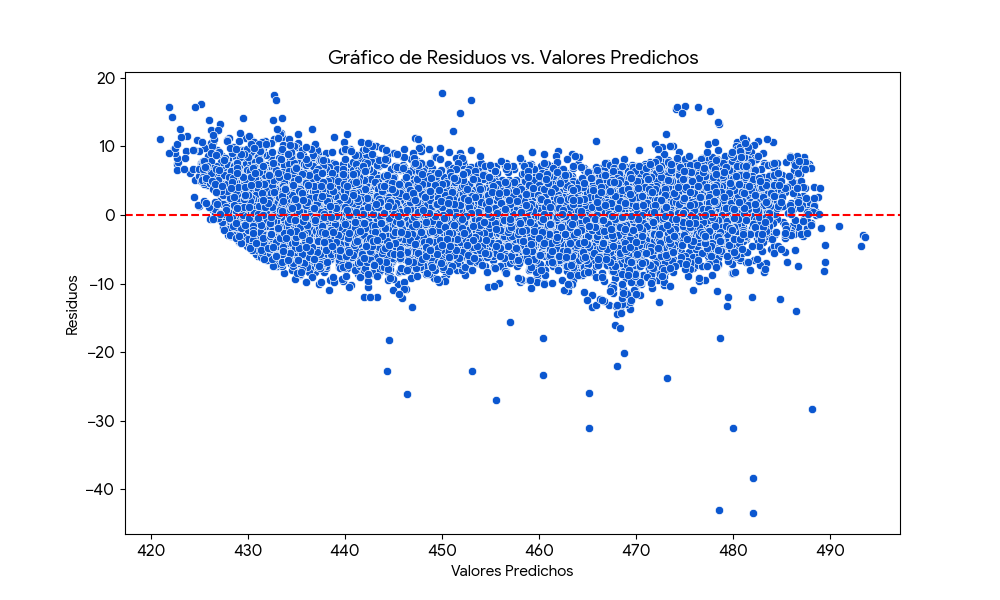
Para verificar la homocedasticidad (varianza constante de los errores), generé un gráfico de los residuos del modelo frente a los valores predichos.
Homocedasticidad: Si los errores tienen una varianza constante, los puntos en el gráfico deberían aparecer distribuidos aleatoriamente, sin un patrón claro, alrededor de la línea horizontal en cero.
Heterocedasticidad: Si los errores no tienen una varianza constante, los puntos formarán un patrón, como un cono o un embudo.
Gráfico de Residuos
Análisis del Gráfico
El gráfico de residuos muestra claramente que la dispersión de los puntos no es constante a lo largo de los valores predichos. A medida que el valor predicho aumenta, la dispersión de los residuos también aumenta, formando un patrón de cono.
Esta forma es un indicio clásico de heterocedasticidad. Esto significa que la varianza de los errores de nuestro modelo no es constante, lo cual viola una de las suposiciones clave de la regresión lineal. La consecuencia es que, aunque nuestras predicciones pueden ser correctas en promedio, las estimaciones de la incertidumbre (intervalos de confianza y pruebas de hipótesis) pueden no ser fiables.




