import pandas as pd
import statsmodels.api as sm
from sklearn.model_selection import train_test_split
data_2 = pd.read_csv('/content/drive/MyDrive/regresion_lineal/usina.csv')
data_2.head()
from sklearn.model_selection import train_test_split
y_ = data_2['PE']
X_ = data_2.drop(columns='PE')
X_train_, X_test_, y_train_, y_test_ = train_test_split(X_, y_, test_size=0.3, random_state=230)
datos_train = pd.DataFrame(X_train_)
datos_train['PE'] = y_train_
from sklearn.metrics import r2_score
X_train_.head()
X_train_ = sm.add_constant(X_train_)
# Previsión con el modelo 0
modelo_energia_0 = sm.OLS(y_train_, X_train_[['const', 'AT', 'V', 'AP', 'RH']]).fit()
X_test_0 = sm.add_constant(X_test_[['AT', 'V', 'AP', 'RH']])
y_predict_ = modelo_energia_0.predict(X_test_0)
print(f'El coeficiente de determinación R² para el modelo con los datos de prueba es de: {round(r2_score(y_test_, y_predict_),2)}')
# Modelo 1: solo AT
modelo_energia_1 = sm.OLS(y_train_, X_train_[['const','AT']]).fit()
# Modelo 2: AT y V
modelo_energia_2 = sm.OLS(y_train_, X_train_[['const','AT', 'V']]).fit()
# Modelo 3: AT, V y AP
modelo_energia_3 = sm.OLS(y_train_, X_train_[['const','AT', 'V', 'AP']]).fit()
# Modelo 4: AT, V y RH
modelo_energia_4 = sm.OLS(y_train_, X_train_[['const','AT', 'V', 'RH']]).fit()
# Creamos una lista con todos los modelos para imprimir sus resúmenes de forma ordenada
modelos_energia = [modelo_energia_0, modelo_energia_1, modelo_energia_2, modelo_energia_3, modelo_energia_4]
# Imprimimos el resumen estadístico de cada modelo para comparar sus resultados
for i,j in enumerate(modelos_energia):
print(f'******************************************************************************\n******************* El modelo {i} tiene el siguiente resumen *******************\n******************************************************************************')
print(j.summary(),'\n\n')
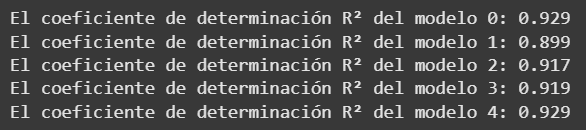
for i, j in enumerate (modelos_energia):
print(f'El coeficiente de determinación R² del modelo {i}: {j.rsquared.round(3)}')
from statsmodels.stats.outliers_influence import variance_inflation_factor as vif
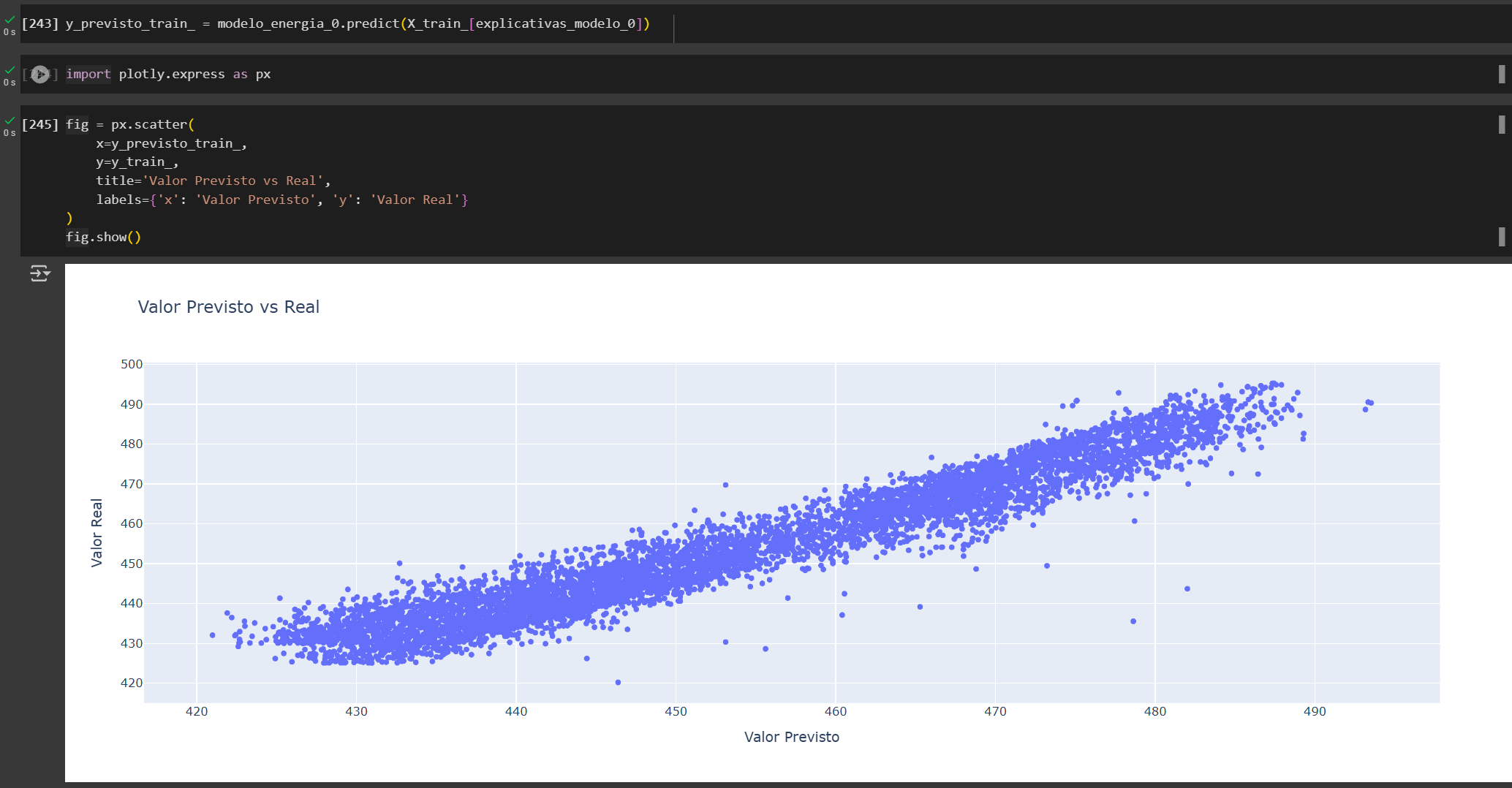
Modelo 0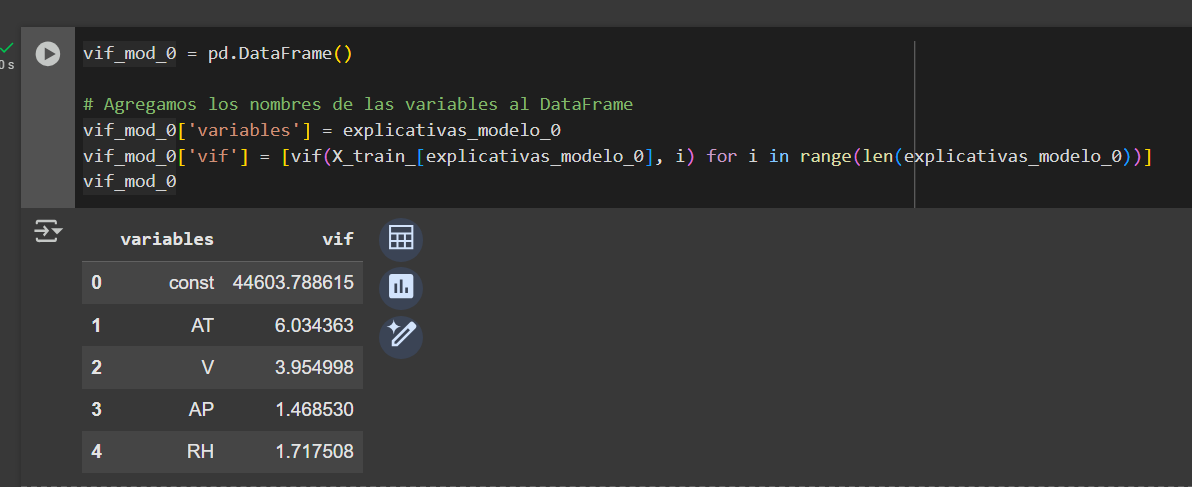
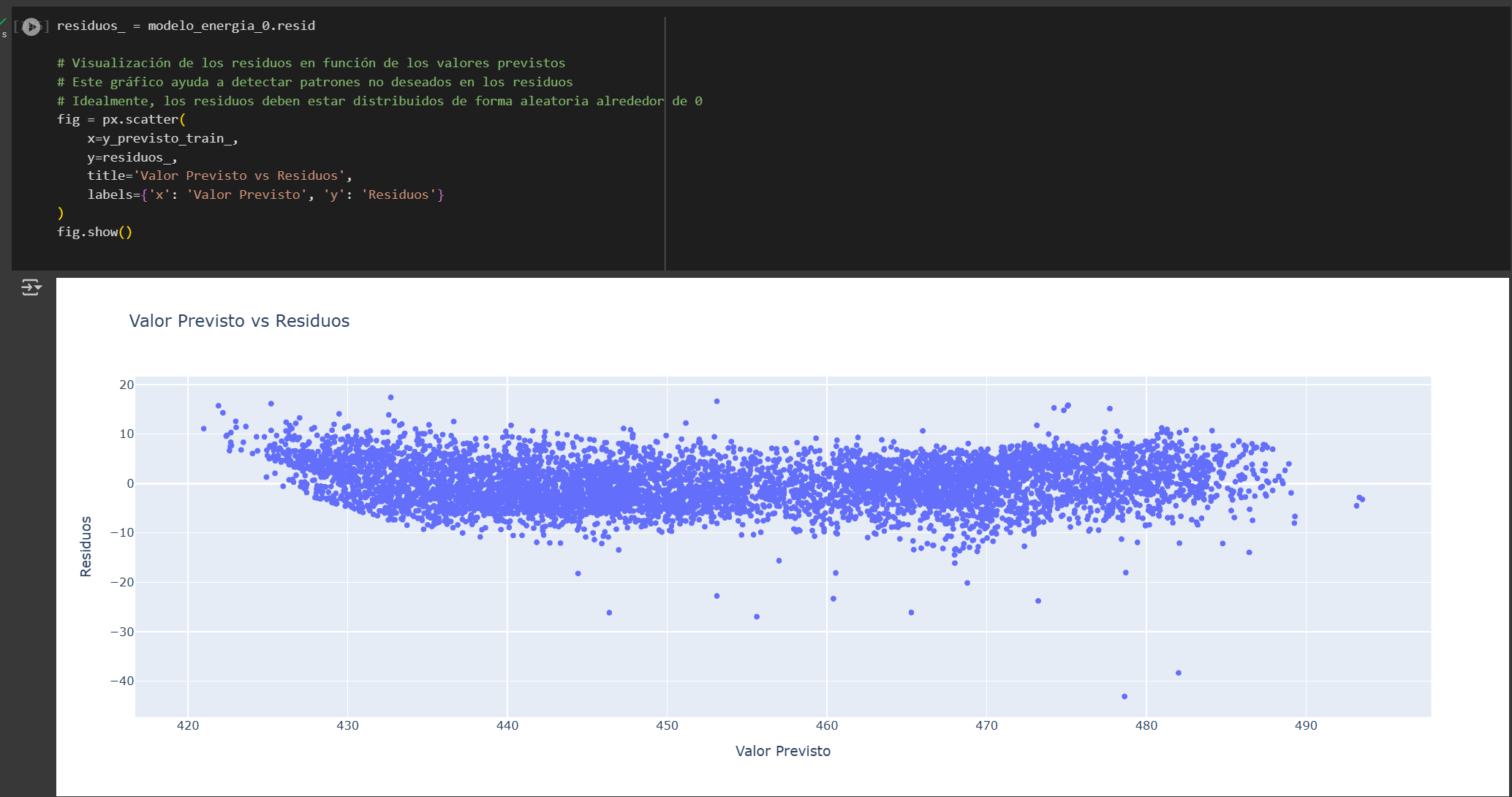
Modelo 4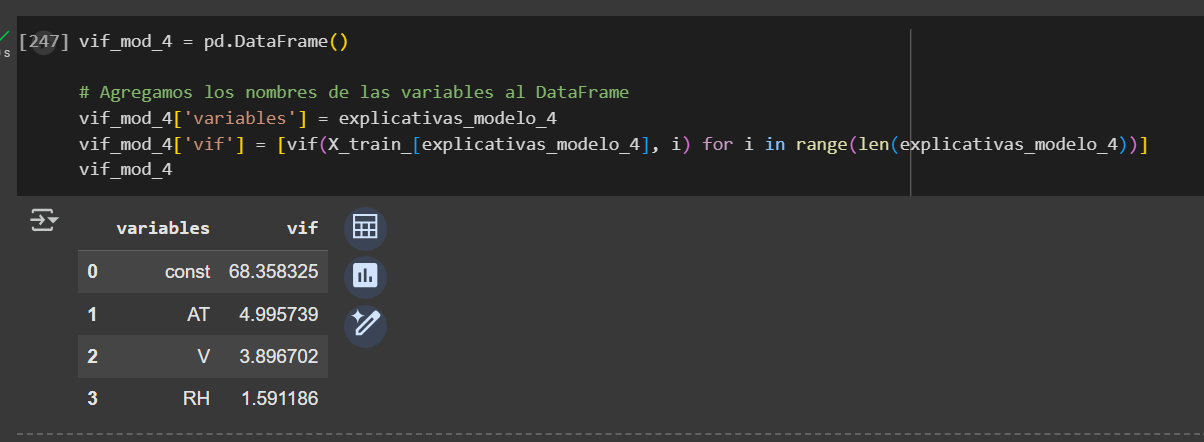
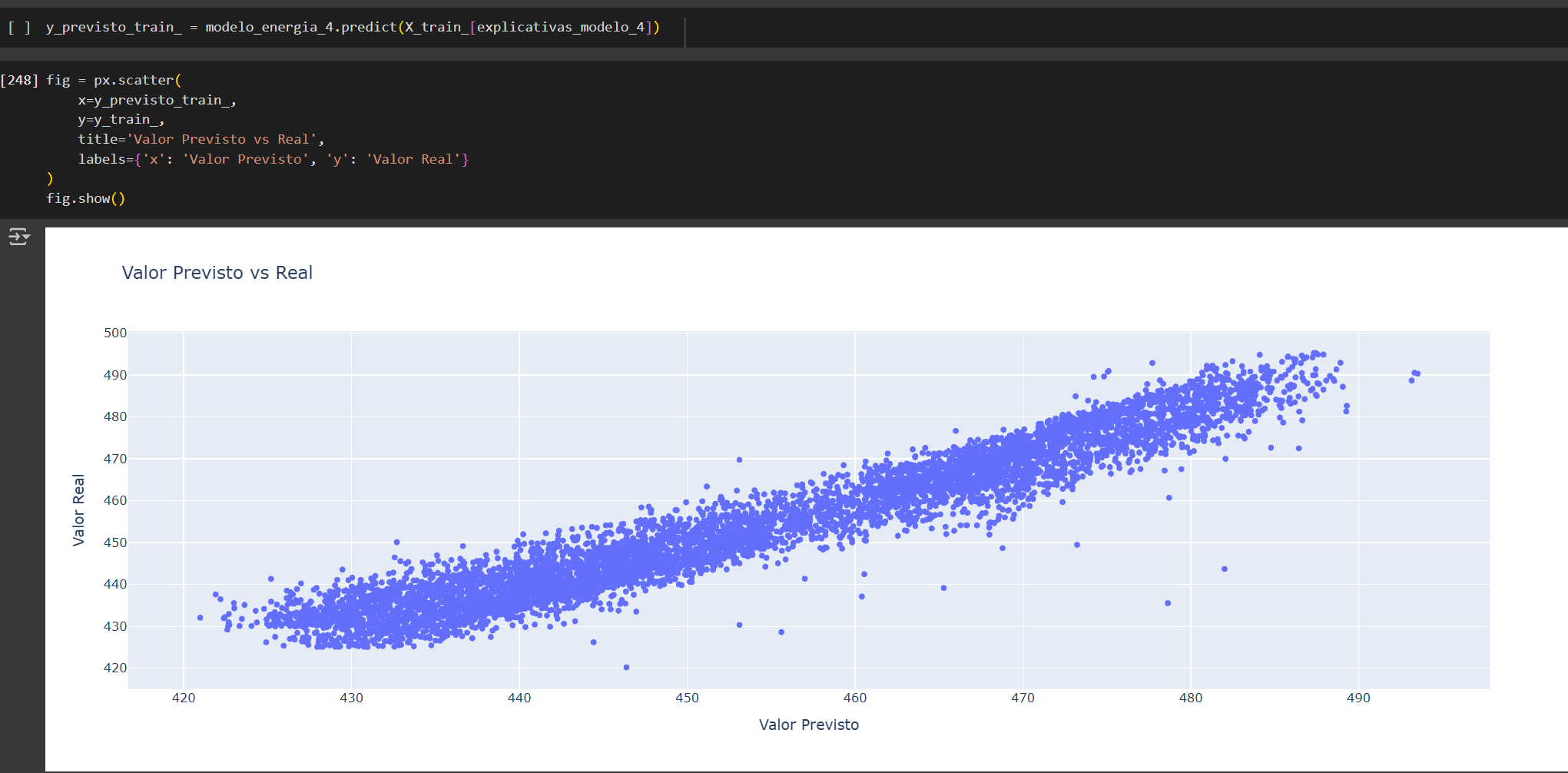
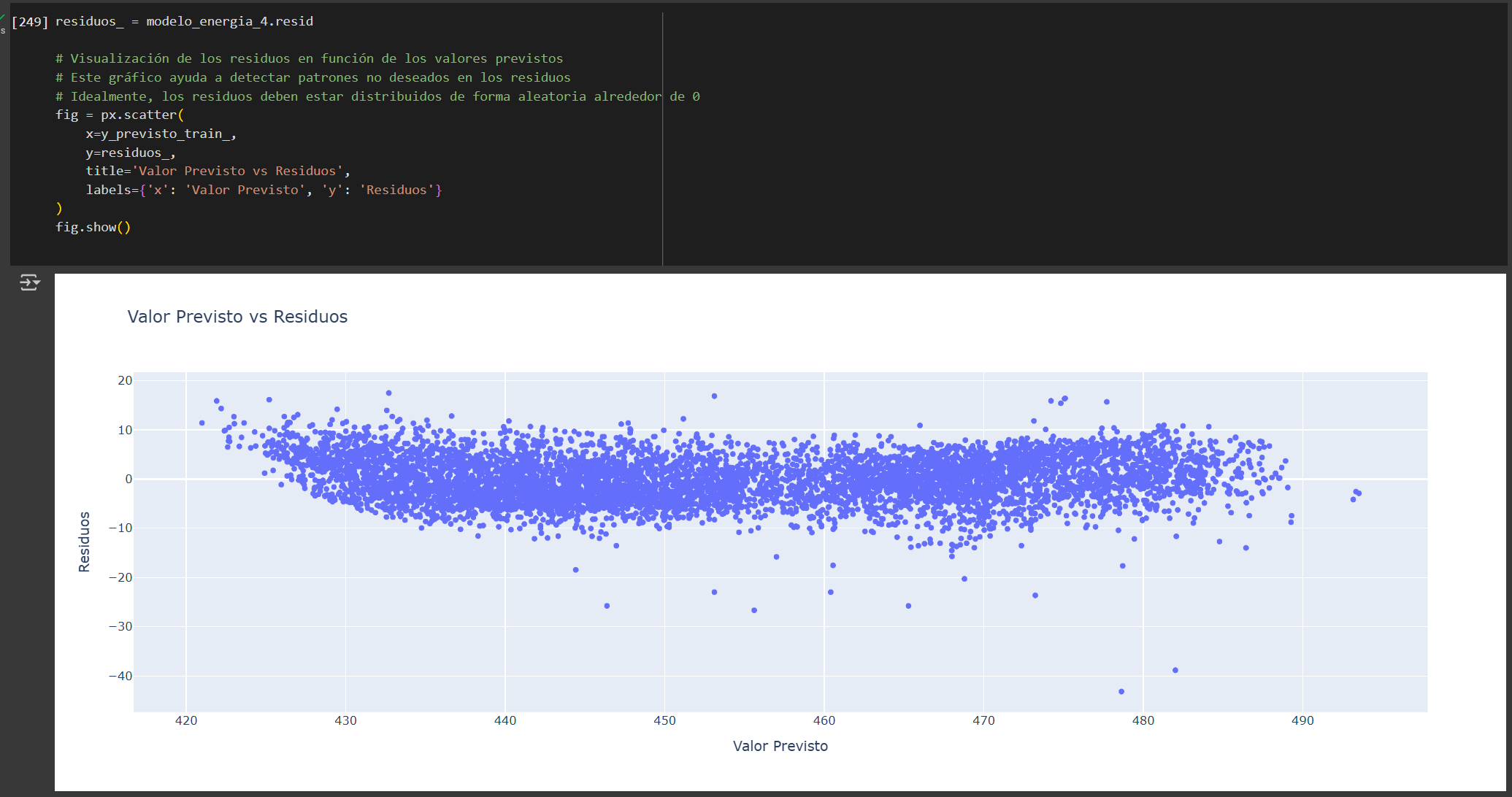
Conclusión:
De los modelos evaluados, el modelo 4 (AT, V y RH) resulta el más adecuado, ya que alcanza un R² de 0.929, equivalente al modelo más complejo (Modelo 0), pero utilizando menos variables.
Además, presenta menor multicolinealidad y una distribución más uniforme de los residuos en torno al eje horizontal, lo que sugiere un mejor cumplimiento de la homocedasticidad en comparación con el Modelo 0.
Si bien ambos modelos muestran una leve heterocedasticidad, los residuos se concentran principalmente entre -10 y 10, por lo que cualquiera de los dos podría utilizarse. Sin embargo, el modelo 4 es preferible por su simplicidad y eficiencia.



