Naranjas

np.random.seed(80)
# Inicializa un array vacío para guardar los errores (distancias) de cada pendiente.
distancia_euclidiana_n = np.array([])
# Genera 120 pendientes aleatorias entre 0 y 30.
pendientes_aleatorias_n = np.random.uniform(0,30,120)


for i in range(len(pendientes_aleatorias_n)): # Recorre las 120 pendientes generadas
  distancia_euclidiana_n = np.append(distancia_euclidiana_n, np.linalg.norm(yn - (pendientes_aleatorias_n[i]*xn+bn)))

print(f"Distancia Euclidiana:\n {distancia_euclidiana_n} \n")
print(f"Pendientes:\n {pendientes_aleatorias_n}")

datos_n = np.column_stack([distancia_euclidiana_n,pendientes_aleatorias_n])
datos_n

# Guarda el array datos en un archivo CSV distancia_euclidiana_y_pendiente_naranjas.csv
# Ubicado en la carpeta especificada, utilizando comas como separador de valores
np.savetxt("/content/drive/MyDrive/Numpy/distancia_euclidiana_y_pendiente_naranjas.csv",
           datos_n,header="Distancia Euclidiana,Pendiente",
           delimiter=",",
           fmt="%.2f",  # Redondea a 2 decimales
           comments=''  # Esto evita que numpy agregue un '#' al inicio del header
)

# np.argmin da valor del índice con menor margen de error, selecciona la mejor pendiente aleatoria.
indice_min_dist_n = np.argmin(distancia_euclidiana_n)
mejor_pendiente_n = pendientes_aleatorias_n[indice_min_dist_n]
print(f"Pendiente óptima: {an}")
print(f"Mejor pendiente aleatoria: {mejor_pendiente_n}")
print(f"Distancia mínima: {distancia_euclidiana_n[indice_min_dist_n]}")

# Cálculo de la mejor estimación con la pendiente aleatoria
yn_aleatoria = mejor_pendiente_n * xn + bn

# Mostrar los tres gráficos
import matplotlib.pyplot as plt
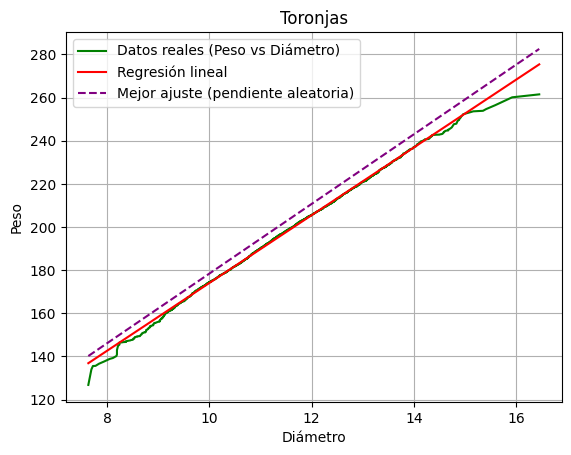
plt.title('Naranjas')
plt.xlabel('Diámetro')
plt.ylabel('Peso')

# Datos reales
plt.plot(diametro_naranjas,peso_naranjas,label="Datos reales (Peso vs Diámetro)",color="#1f77b4") # Línea de datos reales

# Ajuste por mínimos cuadrados
plt.plot(xn, yn, label="Regresión lineal", color="red")

# Ajuste con mejor pendiente aleatoria
plt.plot(xn, yn_aleatoria, label="Mejor ajuste (pendiente aleatoria)", color="purple", linestyle="--")

plt.grid()
plt.legend()
plt.show()

Toronjas

np.random.seed(82)
# Inicializa un array vacío para guardar los errores (distancias) de cada pendiente.
distancia_euclidiana_t = np.array([])
# Genera 120 pendientes aleatorias entre 0 y 30.
pendientes_aleatorias_t = np.random.uniform(0,30,120)


for i in range(len(pendientes_aleatorias_t)): # Recorre las 120 pendientes generadas
  distancia_euclidiana_t = np.append(distancia_euclidiana_t, np.linalg.norm(yt - (pendientes_aleatorias_t[i]*xt+bt)))

print(f"Distancia Euclidiana:\n {distancia_euclidiana_t} \n")
print(f"Pendientes:\n {pendientes_aleatorias_t}")

datos_t = np.column_stack([distancia_euclidiana_t,pendientes_aleatorias_t])
datos_t

# Guarda el array datos en un archivo CSV distancia_euclidiana_y_pendiente_toronjas.csv
# Ubicado en la carpeta especificada, utilizando comas como separador de valores
np.savetxt("/content/drive/MyDrive/Numpy/distancia_euclidiana_y_pendiente_toronjas.csv",
           datos_n,header="Distancia Euclidiana,Pendiente",
           delimiter=",",
           fmt="%.2f",  # Redondea a 2 decimales
           comments=''  # Esto evita que numpy agregue un '#' al inicio del header
)

# np.argmin da valor del índice con menor margen de error, selecciona la mejor pendiente aleatoria.
indice_min_dist_t = np.argmin(distancia_euclidiana_t)
mejor_pendiente_t = pendientes_aleatorias_t[indice_min_dist_t]
print(f"Pendiente óptima: {at}")
print(f"Mejor pendiente aleatoria: {mejor_pendiente_t}")
print(f"Distancia mínima: {distancia_euclidiana_t[indice_min_dist_t]}")

# Cálculo de la mejor estimación con la pendiente aleatoria
yt_aleatoria = mejor_pendiente_t * xt + bt

# Mostrar los tres gráficos
import matplotlib.pyplot as plt
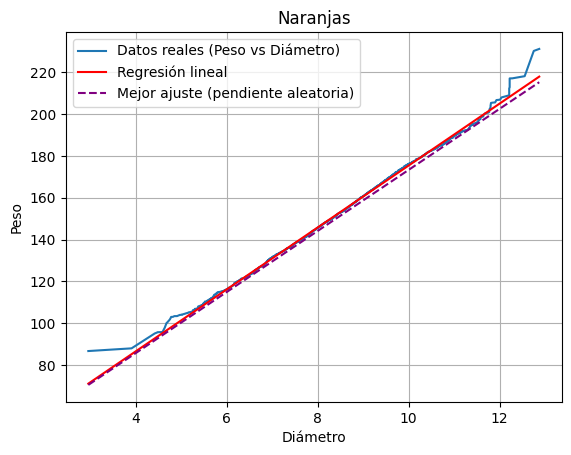
plt.title('Toronjas')
plt.xlabel('Diámetro')
plt.ylabel('Peso')

# Datos reales
plt.plot(diametro_toronjas,peso_toronjas,label="Datos reales (Peso vs Diámetro)",color="green") # Línea de datos reales

# Ajuste por mínimos cuadrados
plt.plot(xt, yt, label="Regresión lineal", color="red")

# Ajuste con mejor pendiente aleatoria
plt.plot(xt, yt_aleatoria, label="Mejor ajuste (pendiente aleatoria)", color="purple", linestyle="--")

plt.grid()
plt.legend()
plt.show()